Spatial and temporal symmetries have been a central theme in designing inclusion-based or periodically arranged metamaterials with desirable wave properties. Inclusion and lattice symmetries enable a rich control of radiative, absorptive and scattering properties of engineered materials. By employing symmetries at both inclusion and lattice levels and considering time-reversal symmetry and non-reciprocal responses, we will develop a general toolkit for the design of metamaterials with extreme wave properties, molding arbitrary interference and diffraction patterns and field profiles in both near- and far-field regions. We will also introduce new concepts stemming from symmetry violations driven by nonlinearities in a variety of wave phenomena.

In this thrust, we will investigate systems with underlying dynamical and hidden symmetries in the evolution equations. Such dynamical symmetries dictate the conservation laws that the system obeys, and hence its dynamics. Among the various dynamical symmetries, parity-time symmetry has been the one spearheading many new developments. PT-wave physics has attracted considerable attention as a powerful mathematical description of classical wave propagation in media with judiciously balanced gain and loss mechanisms, with particularly useful results in purely lossy systems and those with emergent exceptional points (EP). If operated at an EP, a system will experience a sudden change in dimensionality and exhibit a host of unusual responses. This effort will take advantage of the rich opportunities provided by higher-order EP with varying degrees of degeneracy, active systems with EP, multiple EP, and exceptional lines which arise in non-Hermitian photonics crystals where bands merge.

In addition to expanding and generalizing work based on PT symmetry, the team will also investigate other dynamic symmetries to develop new ways to efficiently transport wave packets in space-time, without the need for spatial boundaries or polarization control. One such dynamical symmetry utilizes time-reversal of a steady-state harmonic source to control wave propagation in complex structures. A different approach facilitates waveform design for optimal absorption or transmission using minimal information about the system itself. We will extend the underlying concepts in these cases to the nonlinear regime, where saturation and other phenomena break time and scale invariance. In another case, the team will leverage periodic modulations to build new metamaterial devices that break reciprocity constraints and change the direction of propagation of waves (or wave packets), en route generalizing the fundamental dispersion relations of such time-varying media.

In modern physics, supersymmetry (SUSY) and self-duality have emerged as a way to understand the laws of nature by revealing unexpected links between seemingly unrelated systems. Often this interrelation allows one to gain physical insights into intractable problems, and produce analytical solutions consistent with the constraints imposed by these symmetries.

During this effort, we will identify methods of mapping complex multi-node clusters onto simplified networks, enabling prediction of local nodal state evolution. By doing so, we will achieve dramatic reduction in complexity, dimensionality and connectivity in studying complex networks, even in the presence of nonlinearity. These concepts will be applied to a number of physical settings.

Much like SUSY, dualities also reveal unexpected links between apparently unrelated systems in virtually every branch of physics. Dualities can be understood as a generalization of symmetries when considered within families of theories or models. While symmetries are transformations Φ of a system 𝑆 that leave the system invariant i.e., Φ(𝑆)=𝑆, dualities are transformations that leave invariant a set {S1,S2} of two systems, i.e., Φ(S1)=𝑆2 and Φ(S2)=S1. Self-dual systems are typically associated with the existence of additional symmetries, as the duality transformation usually maps the system to itself in a non-trivial way. Mathematically, these additional symmetries resemble geometrical (crystal) symmetries, but crucially they are not captured by a standard crystallographic analysis based on the space group of the structure. A long-term goal of our effort will be the development of a full classification of dualities and higher-order dualities, including a systematic procedure to generate physical systems endowed with such properties.

Even more powerful approaches can be envisioned by coupling such internal degrees of freedom with those stemming from spatial, unfolded, PT symmetries and synthetic dimensions. Such a multi-symmetry approach will provide a powerful methodology in controlling classical waves where their vectorial degrees of freedom, entangled with one another by symmetries, can be tuned on demand.

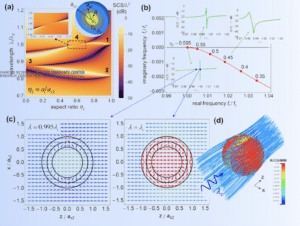
Being able to confine and localize light in small volumes is of paramount importance in several scenarios, e.g., for sensing, data storage and processing. In finite-size open systems, however, any optical state is known to gradually lose its energy by coupling with radiation modes in the surrounding environment, resulting in finite oscillation lifetime. For this reason, light confinement is conventionally achieved by suppressing these radiation channels, “closing” the source region with reflectors or photonic band-gap materials. It has recently been pointed out that ideal optical bound states with infinite lifetime may also interestingly exist within the continuum of radiation modes in open unbounded 2D structures (photonic crystal slabs) [1], in analogy with so-called “embedded eigenstates” in quantum systems [2]. These setups however require infinitely large apertures. In recent works [3]-[4], Silveirinha and our group independently showed that ideal light confinement can be surprisingly achieved also in finite-size three-dimensional open structures, even in the presence of symmetry-compatible radiation channels.Notably, we have theoretically demonstrated ideal light trapping with infinite lifetime in open metallo-dielectric nanocavities in the limit of vanishing material loss. It was previously shown that composite multi-layered nanoparticles may exhibit Fano scattering resonances, arising from the interference of different plasmon modes [5]. Interestingly, we observed that, by varying the composition of plasmonic and dielectric materials, the resonance lifetime of these resonances can diverge at specific singular frequencies (a), as the coupling to free-space radiation is suppressed.This feature represents the fingerprint of an optical bound state with zero radiation loss – and therefore infinite lifetime – remarkably realized in an open system without altering the photonic density of states of the surrounding environment. Our investigations shed light on the generation and dynamics of these embedded scattering eigenstates existing within the radiation continuum (b). This phenomenon may lead to extreme light localization and enhancement (see animations), as the impinging energy is trapped in a self-sustained power flow within the open cavity (c-d). These findings demonstrate a fundamental mechanism for light confinement in open systems, enabled by plasmonic materials, with exciting possibilities for enhanced nonlinearities, thermal ablation, nanolasing, data storage and sensing.

 

[1]C.W. Hsu et al. Nature 499, 188 (2013).

[2]F.Capasso et al. Nature 358, 565 (1992).

[3]M.G. Silveirinha, Phys. Rev. A 89, 023813 (2014).

[4]F.Monticone and A.Alù, Phys. Rev. Lett. 112, 213903 (2014).

[5]F.Monticone et al. Phys. Rev. Lett. 110, 113901 (2013)

Metasurfaces have been establishing a powerful platform for optical wavefront control and manipulation. Their functionalities are typically determined by their tailored local response: subwavelength elements locally imprint the desired pattern of phase and amplitude across the metasurface aperture to realize focusing, beam steering, holograms, and other operations. While this patterning can be achieved with deeply subwavelength spatial resolution, the associated frequency response is difficult to control, resulting in inefficient and unwanted scattering across a broad bandwidth. In contrast, we recently introduced a paradigm to extend metasurface principles to nonlocal responses, enabling exotic wavefront manipulation highly selective to the excitation of interest.

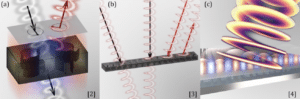
One hallmark of optical nonlocality is the Fano resonance, a phenomenon strongly selective to incoming frequency and momentum, established when a bright resonance couples to a dark mode, e.g., supported by an array of identical subwavelength elements [1]. While this spatial uniformity ensures well-defined nonlocal resonant responses, it precludes the complex spatial manipulation of optical wavefronts peculiar of metasurfaces. We recently presented a rational design overcoming this limitation by applying tailored symmetry-breaking perturbations in an otherwise uniform array. The resulting devices can exhibit full circular dichroism [2] with unity reflectance, and simultaneously support custom geometric phase patterning (Fig. 1a). The arbitrarily polarized resonant states of these nonlocal metasurfaces can be locally controlled with subwavelength resolution, offering exquisite control of the scattering phase across the metasurface and establishing the key building block to extend metasurface concepts to nonlocal responses.

Slightly detuned frequencies negligibly excite these structures, implying a highly selective response. While conventional Fano resonances are selective only to specific plane waves, our nonlocal metasurfaces can be made selective to custom wavefronts [3] to a degree controlled by design; interestingly, the selected wavefront is phase conjugated after engaging the surface (Fig. 1b). These advances open unique opportunities for applications in augmented reality, nonlinear optics, and secure optical communications.

These nonlocal responses are particularly well suited also to manipulate thermal emission and photoluminescence [4], enabling compact optical sources with tailored spatial and temporal coherence, polarization, directionality, focusing, and even wavefronts with custom spin and orbital angular momentum. These thermal metasurfaces (Fig. 1c) efficiently convert heat into quasi-monochromatic optical wavefronts of choice, realizing the long-term goal of flat optics to compactify designer wavefront generation, including sources, into a single thin film.

 

[1] M. Limonov, M. Rybin, A. Poddubny, Y. Kivshar, Nat. Photon. 11 543-554 (2017).

[2] A.C. Overvig, N. Yu, A. Alù, Phys. Rev. Lett. 126, 073001 (2021).

[3] A.C. Overvig A. Alù, Adv. Photon. 3, 026002 (2021).

[4] A.C. Overvig, S. Mann, A. Alù, Phys. Rev. X 11, 021050 (2021).

CUNY’s Andrea Alù describes how metamaterials — materials engineered to have properties not found in nature — are paving the way for a wide range of technological advancements, from cellular communications to energy harvesting to radar cloaking. Check out the video here.

Electromagnetic isolators are highly important devices, as typical communication systems are designed in a modular way, i.e., with modules that are supposed to perform certain tasks or process signals in a specific way. Ideally the response of each module should be independent of the other modules to which it is connected to. For this to happen, it is essential to isolate the different modules, allowing only for ‘one-way’, i.e., nonreciprocal, interactions. In electronic circuits, the isolation between different parts of a circuit is often achieved with the help of semiconductor transistors.

Recently, we introduced the idea of imitating the operation of transistors, which are ‘point’ type devices (i.e., with ‘zero’ dimensions) in a three-dimensional material. Inspired by the operation of standard MOSFET-transistors, we showed that the interplay between material nonlinearities and a static electric bias can lead to a linearized electromagnetic response that is both nonreciprocal and non-Hermitian (response with gain/loss).

The MOSFET-metamaterial can exhibit highly exotic physics. For instance, due to the non-Hermitian response, the different field modes in the material do not transport power independently and the interference between two eigenwaves can give rise to a “power beating”, such that the peak amplitude of the wave oscillates with the propagation distance. In particular, the same 3D bulk material may behave either as a gainy material (i.e., giving energy to the wave) or as a lossy material (i.e., dissipating energy), depending on the field polarization. Remarkably, the eigenpolarizations of a MOSFET-metamaterial are not orthogonal contrary to what happens in Hermitian systems. This unique property may be used to design a myriad of novel devices, such as active electromagnetic isolators, polarization dependent active mirrors, terahertz lasers, for disruptive nanophotonic applications.

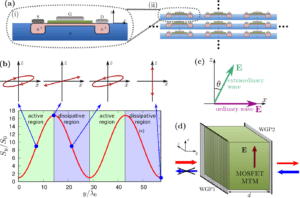
(a)(i) Sketch of a MOSFET transistor. (ii) Illustration of a metamaterial formed by a periodic array of MOSFETs. (b) Normalized Poynting vector as a function of the propagation distance y normalized to the wavelength for an ideal MOSFET-metamaterial. The regions shaded in green correspond to active regions, whereas the regions shaded in purple correspond to dissipative regions. The insets show the field polarization for some points of the curve. (c) Geometrical relation between the E-fields of the plane wave modes in the MOSFET-metamaterial. (d) Electromagnetic isolator based on an electrically biased MOSFET-metamaterial placed in between two orthogonal linear polarizers.

 

[1] S. Lannebère, D. E. Fernandes, T. A. Morgado, and M. G. Silveirinha, “Nonreciprocal and Non-Hermitian Material Response Inspired by Semiconductor Transistors,” Phys. Rev. Lett., vol. 128, p. 013902, 2022.

Topological concepts have emerged in recent years as invaluable tools to characterize the global properties of physical systems. Typically, a nontrivial topology is rooted in some particular symmetry or combination of symmetries of the system, e.g., the system invariance under discrete translations, or the invariance under the time-reversal operation, or others. Topological systems can support either unidirectional propagation channels immune to the undesirable effect of back-reflections due to irregularities and imperfections of the channel. Thereby, topological platforms offer a remarkable playground to explore new physics and phenomena and can lead to unique and exciting applications.

In the case of Chern insulators, the topological properties are rooted in the system periodicity along two directions of real space. In a recent paper [1], we depart from this paradigm and extended the Chern classification to generic one-dimensional (1D)-type photonic platforms. It was demonstrated that a generic non-Hermitian photonic waveguide periodic along a single direction of space can be regarded as a projection in real space of a two-dimensional (2D) topological system with a synthetic dimension. Remarkably, it is shown that the gap Chern number of the extended system with the synthetic dimension is identical to the number of photonic bands below the gap. Furthermore, it was theoretically and numerically demonstrated that in the real space the gap Chern number determines the number of gapless Tamm state branches localized at the system boundary when its geometry is continuously displaced by one lattice period. The operation of a spatial shift by one period may be regarded as a topological pump that inserts topological charge into the system.

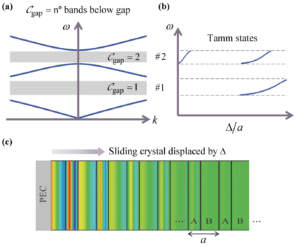
(a) Band structure of a photonic crystal. The gray strips represent the bandgaps and the insets give the gap Chern numbers. (b) Dispersion of the Tamm states localized at an interface between the photonic crystal and a perfect electric conductor (see panel (c)), as a function of the interface cut of the unit cell. The number of Tamm states in each bandgap is exactly coincident with the number of bands below the gap (bulk-edge correspondence). (c) Time snapshot of the magnetic field of a Tamm state.

 

[1] S. V. Silva, D. E. Fernandes, T. A. Morgado, M. G. Silveirinha, “Topological pumping and Tamm states in photonic systems”, Phys. Rev. B 105, 155133 (2022).

In recent years, topological ideas have taken the center stage of modern electromagnetics. Typical topological systems have a broken time reversal symmetry and are based on nonreciprocal materials. Nonreciprocal platforms may enable the unidirectional flow of energy, such that a wave is forced to propagate in a specific direction while the opposite direction does not support light states.

Even though the topological properties of a material are rooted in some abstract mathematical concepts, they can be distilled in a simple physical way. Indeed, consider the problem of interfacing N different nonreciprocal materials at some junction point, as illustrated in panel a). All the materials are operated in a frequency band gap where they do not support propagation in their bulk regions. However, each of the interfaces may support a net number of unidirectional edge states, which can propagate either towards the junction point or away from it. Stating that a system is topological is a sophisticated way of saying that in the described situation it is impossible to devise a construction analogous to that of Fig. 1a with the number of incoming radiation channels being different from the number of outgoing channels. In other words, in topological systems there is forcibly a balance between the number of incoming channels and the number of outgoing channels, analogous to the conservation of current in Kirchhoff’s circuit laws. In fact, if the number of incoming and outgoing channels could be different, then it would be possible to devise an excitation which would continuously transfer energy from a source to the junction point. In such a situation, a thermodynamic equilibrium can be reached only if the energy arriving at the junction is dissipated as heat.

Surprisingly, in Ref. [1] our team experimentally verified that the contrived scenario discussed in the previous paragraph can be observed in realistic physical systems with an “ill-defined” topology, for example in nonreciprocal waveguides with a continuous translation symmetry. It was shown that contrary to common belief, a junction of nonreciprocal materials is not necessarily bound by the constraint that the number of incoming channels must be identical to the number of outgoing channels.  In particular, it was experimentally verified that by pairing two waveguides, one with an ill-defined topology, and another with a well-defined topology, it is possible to bring an edge mode to an immediate halt at the junction between the waveguides, creating a topological singularity as shown in panel b). The wave is stopped on its tracks at the singularity, which can be pictured as an energy sink where all the incoming energy is concentrated and eventually dissipated at a single point in space. These exciting developments suggest that systems with topological singularities can feature extreme wave phenomena and may be useful for energy harvesting and to enhance nonlinear effects.

a) Junction between different bulk materials that share a common band-gap. In a topological system, the number of incoming edge channels and the number of outgoing edge channels is exactly the same.

b) A system with an ill-defined topology is not bound by the constraint in panel a). The ill-defined topology can be used to abruptly halt the wave propagation at a topological singularity with a massive field enhancement.

 

[1] D. E. Fernandes, R. A. M. Pereira, S. Lannebère, T. A. Morgado, M. G. Silveirinha, “Experimental Verification of Ill-defined Topologies and Energy Sinks in Electromagnetic Continua”, Advanced Photonics, 4(3):35003, 2022.

https://www.quantamagazine.org/wheel-made-of-odd-matter-spontaneously-rolls-uphill-20220615/